Spontaneous Symmetry Breaking and the Topology of its Topological Defects

Many fields in particle physics and statistical field theory obey an effective potential which has different minima at different temperatures. For example, the effective potential may behave as $V_\text{eff} \propto \phi^2$ above a critical temperature $T_\text{crit}$ and $V_\text{eff} \propto (\phi^2 - 1)^2$ below this temperature. The changing of minima as temperature cools, known as spontaneous symmetry breaking, can lead to a field taking on different vacuum expectation values $\braket\phi\equiv\braket{0|\phi|0}$ at different regions in spacetime below the critical temperature.

Because these vacuum expectation values are continuous over spacetime, they can have nontrivial topology whose topological defects exhibit dynamical behavior. Examples of topological defects include domain walls, cosmic strings, and charge monopoles. The large scales and high energy densities of these defects may give them a role in the formation of structure in the early universe.

To be generic, we will describe topological defects in a general $N$-component real Lorentz scalar¹ field $\phi = (\phi_1,\cdots,\phi_N) : \mathcal S\to\R^N$ on the Minkowskian spacetime manifold $\mathcal S \equiv \R^{3+1}$. This can be used to model scalar and pseudoscalar fields, such as the Higgs boson and the QCD axion.

Spontaneous symmetry breaking

If we demand the Lagrangian of $\phi$ to be renormalizable² (which restricts the highest power of $\phi$ to 4) as well as invariant under local $O(N)$ transformations³ (which restricts $\phi$ and its derivatives to always come in contracted pairs, e.g. $\phi^2 \equiv \phi_i \phi_i$), then the most general Lagrangian for this field looks like \[\begin{equation} \mathcal L = \f12(\p_\mu \phi)^2 - V_\pm,\quad \text{where } V_\pm = \pm\f12 m^2 \phi^2 + \f14\lambda \phi^4. \end{equation}\]

Should we pick the $V_+$ solution, then the only minimum exists at the origin. In correspondence with classical mechanics, the vacuum expectation value of the field then settles here: $\braket{\phi} = 0$. This zero field is invariant under $O(N)$ gauge transformations, the same group as the Lagrangian, so we say all the gauge symmetries in our theory is manifest.

Should we instead pick the more interesting $V_-$ solution, then when the temperature $T=0$, the field’s vacuum expectation value $\braket{\phi}$ settles down at a nonzero value constrained by $\braket{\phi}^2 = \mu^2$, where $\mu \equiv m/\lambda$. But any nonzero element of $\R^N$ is only invariant under $O(N-1)$,⁴ not the full Lagrangian symmetry $O(N)$, so we say our field breaks or hides a symmetry of our theory.⁵ The set of available vacuum expectation values forms a manifold of degenerate vacua $\mathcal M$, which is the orbit of $\braket\phi$ under $O(N)$. This manifold is an $(N-1)$-sphere because by the orbit-stabilizer theorem, \[\begin{equation} \mathcal M = \mathrm{Orb}\brk{O(N)} = \f{O(N)}{\mathrm{Stab}\brk{O(N)}} = \f{O(N)}{O(N-1)} = S^{N-1}. \end{equation}\]

Let’s see why this makes sense. For an $(N=1)$-component scalar field, every physical point in spacetime picks either $\braket\phi = +\mu$ or $\braket\phi = -\mu$ as its vacuum, so the manifold of degenerate vacua is the set of two disconnected points corresponding to the two minima in Fig 1. This indeed agrees with Eqn (2)’s prediction that $\mathcal M$ is the zero-sphere. For an $(N=2)$-component real scalar field $\phi = (\phi_1, \phi_2)$ (or equivalently, a complex scalar field), the manifold $\mathcal M = S^1$ is a circle of degenerate vacua constrained by $|\!\braket\phi\!| = \mu$. For $N=3$, $\mathcal M = S^2$, and so on.

So far, we have characterized the vacuum at absolute zero temperature. However, if we raise the temperature, then the system minimizes free energy instead of total energy, and the potential effectively becomes \[\begin{equation} V_\text{eff} = -\f12 m^2\phi^2 + \f14\lambda\phi^4 + \f{N+2}{24}\, T^2 \phi^2. \end{equation}\] A short calculation shows that the hidden symmetry of the theory is restored in $\braket\phi$ above the critical temperature \[\begin{equation} T_\text{crit} = \mu\sqrt{\f{12}{N+2}}, \end{equation}\] when $V_\text{eff}$ returns to having one single minimum at $\braket\phi=0$.

Topological defects

Globally, the field energy $V(\braket\phi)$ is minimized when $\braket\phi^2 = \mu^2$ everywhere in space. However, starting from arbitrary initial conditions, this ground state not always reached. In many situations, there exist concentrations of high energy in the field, known as solitons, which cannot be destroyed as long as the temperature $T < T_\text{crit}$. The topology of the degenerate vacua $\mathcal M$ determines the structure of these solitons that appear in physical spacetime, which is why they are also more specifically referred to as topological defects.

Domain walls

In the $N=1$ case with a two-point degenerate vacua $\mathcal M = S^0$, the prototypical example in statistical field theory is the Ising model of ferromagnetization, where $\phi: \mathcal S\to\R^1$ is a field of the $z$-component of angular momentum, with $\braket{\phi} = \pm\mu \in \mathcal M$ corresponding to a point in spacetime being either spin-up or spin-down at the minima of the potential. Neighboring regions of spacetime prefer to have the same vacuum expectation value, because for $\phi$ to be a continuous field, somewhere between a region where $\braket\phi=-\mu$ and a region where $\braket\phi=+\mu$, $\braket\phi$ must exit the minimum of $V(\braket\phi)$ and take on a value $\braket\phi=0$ which lies on the central maximum of the potential. In other words, neighboring spins like to be aligned because an anti-alignment would raise the energy.

We can prove the existence of this high-energy region with homotopy, the study of contracting manifolds on other manifolds. Proof: Supposing instead that $V(\braket\phi)$ is minimized everywhere in space, then any point in space, the $\braket\phi$ can be identified with a single point in $\mathcal M$. However, if we test two points in space, and they identify with the two different points in $\mathcal M$, then as we bring the two test points together in space, we are contracting the two points in $\mathcal M$ onto one. This means on $\mathcal M = S^0$, we can contract the manifold of two points $S^0$ onto a point. In other words, our assumption would imply that $S^0$ is homotopic to a point on $S^0$, i.e. $\pi_0(S^0)$ is trivial. But $\pi_0(S^0)$ is nontrivial, so as long as two different points of space take on different $\braket\phi$, then these concentrated regions of high-energy must exist!

Moreover, since any path connecting the two test points contains some point where $\braket\phi = 0$, this $N=1$-component field produces $K=2$-dimensional domain walls in $D=3$-dimensional space.⁶

Indeed, if we observe $\phi$ as temperature is quickly lowered from above $T_\text{crit}$ to zero, then its random thermal fluctuations at high temperature are almost guaranteed to create regions of different $\braket\phi$ at $T<T_\text{crit}$, with domain walls marking the boundaries between them.

And as we will see, this $K = D-N$ relation holds for other topological defects in the $\R^N$-field model as well.

Cosmic strings

In the $N=2$ case, we find high-energy quantum field theories like the Higgs boson and the QCD axion. At $T<T_\text{crit}$, $\braket\phi$ settles at some phase on the circle of degenerate vacua $\mathcal M = S^1$. Here, like in the Ising model, neighboring in spacetime would prefer to take vacuum expectation values corresponding to neighboring points in $\mathcal M$ to minimize energy. However, random thermal fluctuations can conspire so that if we trace a loop in space, the range of $\braket\phi$ on this loop may cover the entire circle of $\mathcal M$. As we contract this test loop into a point in space, we cannot contract the corresponding loop on $\mathcal M$ onto a point there. This is again a consequence of topology: $S^1$ is not homotopic to a point in $S^1$, i.e. $\pi_1(S^1)$, the fundamental homotopy group on $S^1$, is nontrivial.

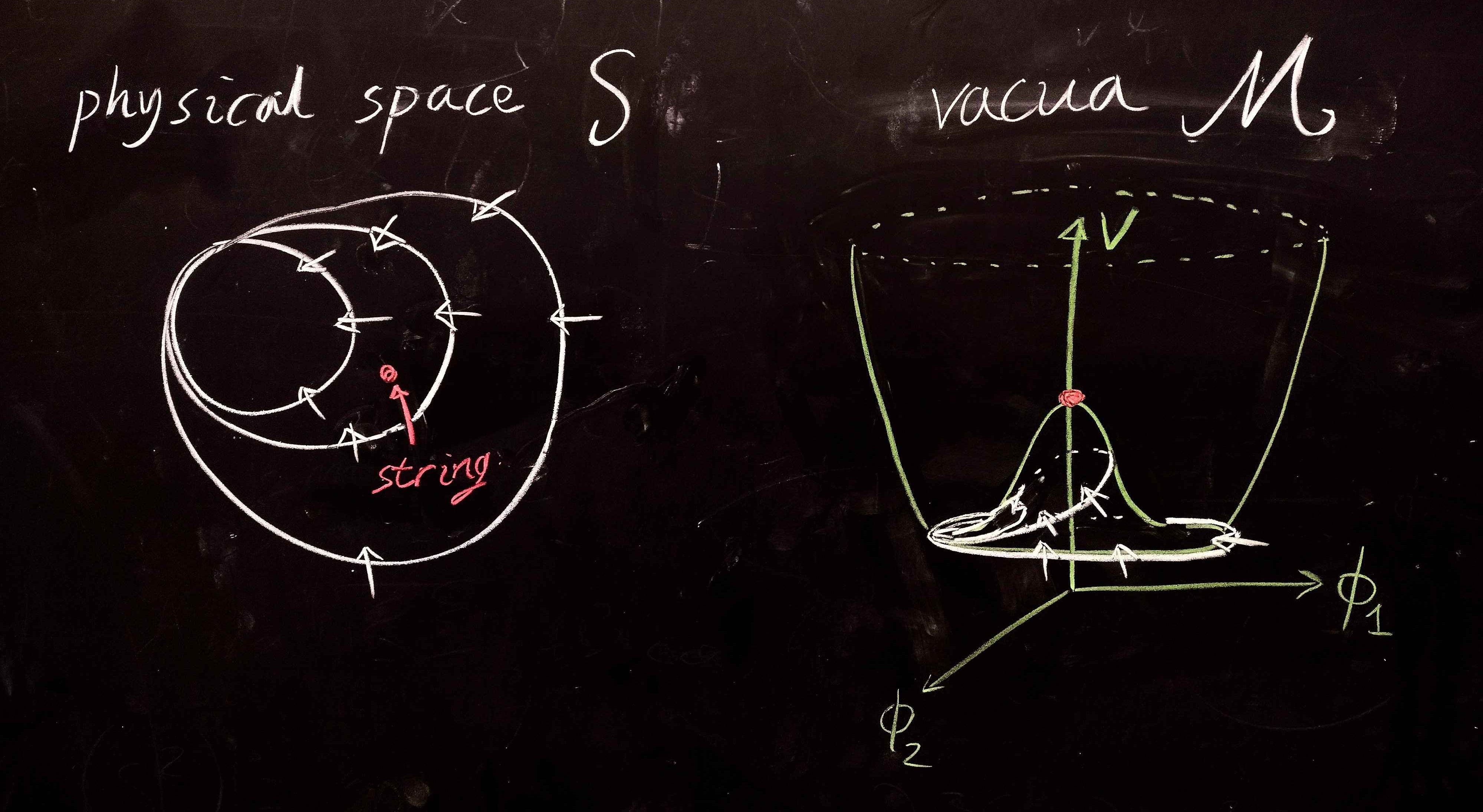
This means that during the contraction of this test loop in space, the corresponding loop of $\braket\phi$ values must exit $\mathcal M$, with one point on the loop passing through a region of high energy. Because this high-energy region holds for any contracting motion of the loop, it is $(K = D - N = 1)$-dimensional: we found a (cosmic) string!⁷

Monopoles

The power of homotopy is that we can play this game with arbitrary-dimensional fields and spacetimes, and exhaustively search for systems where topological defects may be present, even if the dimensions are too large for us to visualize the contractions. With $N=3$, we find that because $\pi_2(S^2)$ is nontrivial, contractions of a test sphere in space can cross a $K=D-N$=0-dimensional region of high energy: a monopole.

I think this has to do with magnetic monopoles. Story for another time.

Acknowledgements

Thanks to Winston Yin for introducing me to cosmic strings, Keshav Deoskar for teaching me homotopy, and Adarsh Iyer for teaching me group theory. I wrote these notes as my final project for the Physics 198 Differential Geometry and Lie Groups DeCal at Berkeley, taught by Michelle Dong, Finn Grathwol, and Keshav. My notes are largely based on the 1976 paper Topology of Cosmic Domains and Strings by T.W.B. Kibble.

Feet